ISS가 달 위를 지나가는 시각을 알 수 있을까요?

알림

BLUEnLIVE 211.♡.234.109

2024.05.06 21:33

227

쓰기

정신 나간(?) 글 3부작의 마지막회입니다. 이번에도 역시 출처는 제 블로그.

아래 사진은 SciTechDaily에 올라온 사진입니다.
인터넷에서는 이처럼 ISS가 달 위를 지나가는 장면을 촬영한 사진을 가끔 볼 수 있어요.

앞의 글들에서 얘기했듯이, 파이썬 라이브러리들을 활용하면 ISS나 달의 위치는 꽤 쉽게 알 수 있습니다.

그렇다면 ISS가 달 위를 언제 지나가는지도 알 수 있을까요?

들어가기에 앞서

이전 글들에서 ISS와 달의 위치를 파악하는 방법을 간단하게 얘기했습니다.

그리고, 그 때 사용했던 라이브러리들을 활용하면 이 문제도 그리 어려워 보일 것 같지 않아요.
(훗, 과연 그럴까?)

달의 시직경은 약 0.5도 입니다.
ISS가 달 위를 지나간다는 얘기는 관측자 위치에서 이 둘을 향해 그은 벡터의 내각이 0.25도 이내란 뜻이에요.

그렇다면, 달이 뜰 때부터 질 때까지의 모든 시간에 대해 이걸 계산하면 되는 거죠.

그런데, 문제는 ISS의 위치예요.

ISS는 TLE를 다운받아 이를 통해 위치를 알 수 있습니다.
그런데, TLE는 특성상 며칠 지나면 정확도가 떨어져요.

즉, 계산을 통해 알 수 있는 ISS의 위치는 하루 이상 지나면 신뢰도가 떨어진다는 뜻이에요.
2주 지난 TLE로 ISS의 위치를 실제로 그려보니 대륙 하나가 벗어나있더군요. (아프리카 ↔ 남아메리카)

기존 코드들의 활용과 확장

ISS의 TLE를 얻어 위치를 산출하는 과정은 이전 글과 동일해요.

그 외에 달에 대한 정보는 astral 라이브러리를 사용하면 됩니다.
이 라이브러리에서는 관측자의 위치를 기준으로 달의 위치는 물론, 뜨고 지는 시간도 알려줍니다.

날짜에 따라서는 뜨거나 지는 시간이 없는 경우도 있으니 이 점도 고려해야 돼요.

from skyfield.api import load
from datetime import timedelta
from astral import moon

def get_iss_object_skyfield():
  satellites=load.tle_file(url='https://live.ariss.org/iss.txt',reload=True)

  iss=satellites[0]

  return iss


def get_moon_rise_moon_set(location,tm):
  try:
    moon_rise=moon.moonrise(location.observer,tm)
  except:
    tm+=timedelta(days=1)
    moon_rise=moon.moonrise(location.observer,tm)

  tm=moon_rise
  try:
    moon_set=moon.moonset(location.observer,tm)

  except:
    tm+=timedelta(days=1)
    moon_set=moon.moonset(location.observer,tm)

  if moon_rise>moon_set:
    tm+=timedelta(days=1)
    moon_set=moon.moonset(location.observer,tm)

  return  moon_rise,moon_set

필요한 함수들의 구현

경위도 좌표를 직교좌표로 변환하는 함수가 우선 필요해요.
우리가 사용하는 거의 모든 좌표는 WGS84 좌표계를 사용한다는 점만 고려하면 됩니다.

import numpy as np

def wgs84_llh_to_xyz(llh):
  lat_rad=np.deg2rad(llh[0])
  lon_rad=np.deg2rad(llh[1])
  alt=llh[2] if len(llh)>2 else 0

  clat=np.cos(lat_rad)
  slat=np.sin(lat_rad)
  clon=np.cos(lon_rad)
  slon=np.sin(lon_rad)

  wgs84_a=6378137.0
  wgs84_finv=298.257223563
  wgs84_f=1/wgs84_finv
  wgs84_e2=1-(1-wgs84_f)*(1-wgs84_f)

  rn=wgs84_a/np.sqrt(1-wgs84_e2*slat*slat)

  x=(rn+alt)*clat*clon
  y=(rn+alt)*clat*slon
  z=(rn*(1-wgs84_e2)+alt)*slat

  return np.array([x,y,z])

ISS의 위치는 직교좌표 형태(x, y, z)로 얻어집니다.

그런데, 달의 위치는 관측자의 위치를 기준으로 하는 방위와 천정각 형태(degree, degree)로 얻어요.
이 둘을 비교하려면 ISS의 위치를 관측자 위치 기준의 방위와 천정각으로 변환해야 합니다.

회전 변환을 위해 쿼터니언(사원수)를 사용하면 편리해요.
쿼터니언을 사용하면 행렬로 표현하는 것보다 훨씬 간단하게 할 수 있어요.

해밀턴 형님 사랑합니다!

from pyquaternion import Quaternion
from astropy import units as u

def calc_azimuth_zenith(my_llh,iss_xyz):
  count=len(iss_xyz)
  ret=np.zeros((count,2),dtype=np.float64)
  my_xyz=wgs84_llh_to_xyz(my_llh)
  lat=np.deg2rad(my_llh[0])
  lon=np.deg2rad(my_llh[1])

  vectors=iss_xyz.to(u.m).value-my_xyz
  # 이 vectors는 lat, lon에서 출발하는 벡터임
  # 이를 경위도 원점(0,0)에서 출발하는 벡터로 회전 변환 필요

  # iss를 경위도 0,0으로 회전시키는 쿼터니언 생성
  q=Quaternion(axis=[0,1,0],angle=lat)*Quaternion(axis=[0,0,1],angle=-lon)

  for i,v in enumerate(vectors):
    v=q.rotate(v)         # vector 회전
    v=v/np.linalg.norm(v) # normalizing

    # azimuth, zenith 계산
    az=180-np.degrees(np.arctan2(v[1],-v[2]))
    ze=90-np.degrees(np.arcsin(v[0]))
    ret[i]=[az,ze]

  return ret

마지막으로 필요한 함수는 방위와 천정각이 주어졌을 때 두 벡터 사이의 각을 계산하는 함수예요.

처음엔 단위 벡터를 만들어 내적을 구하는 방식으로 만들었는데, github copilot 님께서 간단한 방식을 알려주심...

def calc_angle_between(azimuth1,zenith1,azimuth2,zenith2):
  # 모든 각을 radian으로 변환
  azimuth1=np.deg2rad(azimuth1)
  zenith1=np.deg2rad(zenith1)
  azimuth2=np.deg2rad(azimuth2)
  zenith2=np.deg2rad(zenith2)

  cos_theta=np.sin(zenith1)*np.sin(zenith2)*np.cos(azimuth1-azimuth2)+np.cos(zenith1)*np.cos(zenith2)
  theta=np.arccos(cos_theta)

  return np.rad2deg(theta)

본체 구현

실제로 구현해야 할 내용은 다음과 같아요.

주어진 날짜의 달이 뜨고 지는 시간 계산
이 시간에 대해 달의 방위 계산
이 시간에 대해 ISS의 위치 계산
ISS의 위치를 관측자의 위치 기준의 방위로 변환
두 점 사이의 각 계산

계산할 내용이 적지 않기 때문에 시간 간격이 짧아질수록 시간이 훨씬 많이 소요됩니다.
물론, 정확도는 높아지겠죠.

일단 달이 뜨고 지는 시간을 계산하는 코드는 다음과 같아요.

시간 간격은 0.5초로 했습니다. 계산이 너무 오래 걸리면 이 값을 늘리면 돼요.

from datetime import datetime
from pytz import timezone,utc
import matplotlib.pyplot as plt
from astral import LocationInfo

observer_lat=37.46707105652381
observer_lon=127.07507550716402
observer_alt=73.0
step_in_second=0.5  # 0.5초 간격으로 달이 뜨는 시각부터 지는 시각까지의 시각을 구한다.
days_after=0        # 며칠 뒤를 계산할 것인지

location=LocationInfo(name="Seoul",region="Korea",timezone="Asia/Seoul",latitude=observer_lat,longitude=observer_lon)
tm=datetime.now(tz=utc)+timedelta(days=days_after)

print('현재 시각:     ',tm.astimezone(timezone(location.timezone)))

moon_rise,moon_set=get_moon_rise_moon_set(location,tm)
print('달 뜨는 시각:  ',moon_rise.astimezone(timezone(location.timezone)))
print('달 지는 시각:  ',moon_set.astimezone(timezone(location.timezone)))

duration=int((moon_set-moon_rise).total_seconds())
print('달 떠있는 시간:',duration,'초')

print('---------------------------------')

다음으로 주어진 시간에 대해 달의 방위각, 천정각을 계산할 차례.
참고로, 천정각은 90도에서 고도를 뺀 값의 개념이에요.

# 주어진 시간에 대해 달의 방위각, 천정각을 구한다.
moon_times=[]

for i in np.arange(0,duration,step_in_second):
  moon_times.append(moon_rise+timedelta(seconds=i))

moon_az=np.zeros(len(moon_times))
moon_ze=np.zeros(len(moon_times))

for i,mt in enumerate(moon_times):
  moon_az[i]=moon.azimuth(location.observer,mt)
  moon_ze[i]=moon.zenith(location.observer,mt)

그 다음은 ISS의 방위각, 천정각을 계산.
ISS의 직교좌표(XYZ)를 구하고, 이를 관측자의 위치를 기준으로 방위각, 천정각으로 변환합니다.

# 주어진 시간에 대해 ISS의 XYZ 좌표를 구한다.
ts=load.timescale()
moon_times=ts.from_datetimes(moon_times)

iss=get_iss_object_skyfield()
iss_geocentric=iss.at(moon_times)
iss_xyz=iss_geocentric.itrf_xyz().to(u.m)
iss_xyz=iss_xyz.transpose()

# ISS의 XYZ 좌표를 이용하여 azimuth, zenith를 구한다.
iss_az_ze=calc_azimuth_zenith((observer_lat,observer_lon,observer_alt),iss_xyz)

iss_az=iss_az_ze[:,0]
iss_ze=iss_az_ze[:,1]

마지막으로 두 각들의 사잇각을 계산하면 끝입니다.

# 달과 ISS의 사잇각을 구한다.
angles=calc_angle_between(moon_az,moon_ze,iss_az,iss_ze)

# moon_times 값들을 local 시간으로 변환한다.
moon_times=[mt.astimezone(timezone(location.timezone)) for mt in moon_times]

# angles가 최솟값인 시각을 찾는다.
min_angle=np.min(angles)
min_index=np.argmin(angles)
min_time=moon_times[min_index]

print('달과 ISS 사이가 가장 가까운 각도:',min_angle)
print('달과 ISS 사이가 가장 가까운 시각:',min_time)

my_xyz=wgs84_llh_to_xyz((observer_lat,observer_lon,observer_alt))
min_iss_pos=iss_xyz[min_index].to(u.m).value
min_iss_xyz=min_iss_pos-my_xyz
min_distance=np.sqrt(min_iss_xyz[0]**2+min_iss_xyz[1]**2+min_iss_xyz[2]**2)
print('그 때 ISS 까지의 거리:          ',min_distance/1000,'km')
print('그 때 ISS의 방위각:             ',iss_az[min_index],'도, 천정각:',iss_ze[min_index],'도')


## 그래프 그리기
plt.plot(moon_times,angles)
plt.xlabel('Date/Time')
plt.ylabel('Angle between Moon and ISS')
plt.title('Angle between Moon and ISS')

plt.show()

계산 결과

실행 결과는 다음과 같아요.

달과 ISS 사잇각이 가장 작은 시각은 4월 8일 09시 42분 32.5초로, 이 때의 각도는 4.69도.
백주대낮이니 달이 제대로 보이진 않았을 겁니다...

현재 시각:      2024-04-07 18:23:46.015400+09:00
달 뜨는 시각:   2024-04-08 05:45:00+09:00
달 지는 시각:   2024-04-08 18:30:00+09:00
달 떠있는 시간: 45900 초
---------------------------------
[#################################] 100% iss.txt
달과 ISS 사이가 가장 가까운 각도: 4.694649913207852
달과 ISS 사이가 가장 가까운 시각: 2024-04-08 09:42:32.500000+09:00
그 때 ISS 까지의 거리:           543.9669704560661 km
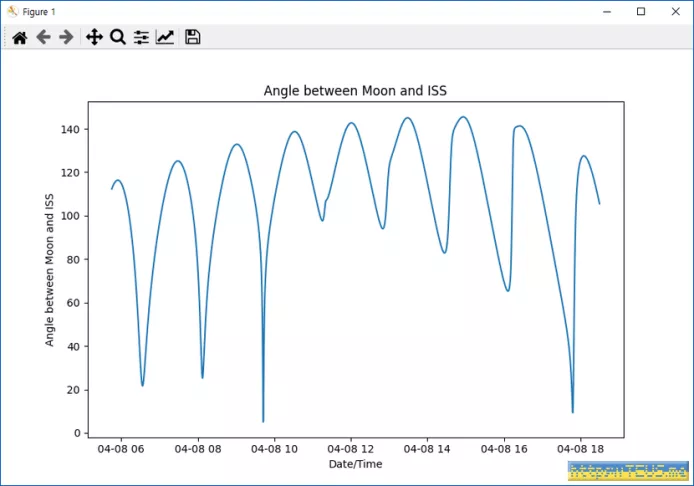
그 때 ISS의 방위각:              129.85901531930875 도, 천정각: 41.67761609274922 도

시간에 따른 사잇각의 그래프는 아래와 같아요.