의외로 인류가 아직도 완전히 풀지 못한 수학 문제
알림
|
페이지 정보
작성일
2024.11.12 10:32
본문
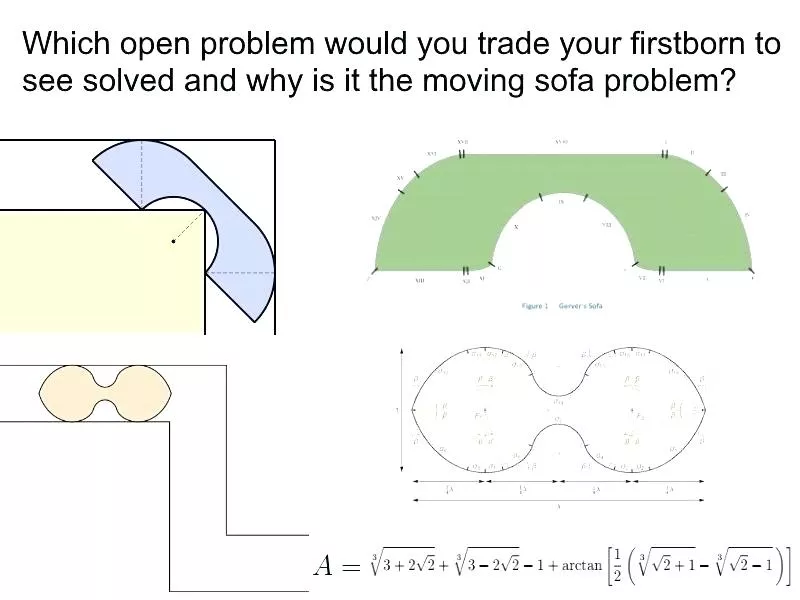
The Moving sofa problem
폭이 1m이고 직각 커브가 있는 복도를 지날 수 있는 도형의 최대 넓이를 구하는 문제입니다.
2차원이어야 한다는 점을 빼면 문제 해결을 위한 도형의 형태에 전혀 제한이 없음에도 불구하고 현재까지 최대 크기가 얼마인지 밝혀내지 못했죠.
댓글 9
/ 1 페이지
Drum님의 댓글의 댓글
@제리아스님에게 답글
이게 실상은 최댓값을 찾는 문제라기 보다는 현재까지 발견 한 최댓값이 진짜 최댓값이 맞는지 증명을 하지 못 한 성격의 문제입니다.
일단 여러 학자들이 보기에 이게 최댓값은 맞는 것 같은데... 정말 이게 끝일까? 하는 의문이 명확하게 밝혀지지 않은거죠.
일단 여러 학자들이 보기에 이게 최댓값은 맞는 것 같은데... 정말 이게 끝일까? 하는 의문이 명확하게 밝혀지지 않은거죠.
벗님님의 댓글
gemini를 어르고 달랬더니, 이런 코드까지는 만들어주네요.
*
import numpy as np
import matplotlib.pyplot as plt
# 상수 정의
CORRIDOR_WIDTH = 1 # 복도 폭
MAX_ITERATIONS = 1000 # 유전 알고리즘 반복 횟수
POPULATION_SIZE = 100 # 개체 수
# 소파 표현 (다각형)
def create_sofa(num_sides):
# ... (생략)
# 소파 회전
def rotate_sofa(points, angle):
# ... (생략)
# 충돌 검사 (복도를 두 개의 직선으로 나누어 검사)
def check_collision(sofa_points, corridor):
# ... (생략)
# 다각형 면적 계산 (가우스의 끈 공식)
def calculate_polygon_area(points):
x = points[:, 0]
y = points[:, 1]
return 0.5 * np.abs(np.dot(x, np.roll(y, 1)) - np.dot(y, np.roll(x, 1)))
# 적합도 함수
def calculate_fitness(sofa_points, corridor):
area = calculate_polygon_area(sofa_points)
if check_collision(sofa_points, corridor):
area *= 0.5
return area
# 유전 알고리즘
def genetic_algorithm(population, fitness_func, corridor, max_iterations):
for generation in range(max_iterations):
# 선택 (토너먼트 선택)
# ...
# 교차
# ...
# 돌연변이
# ...
return max(population, key=lambda x: fitness_func(x, corridor))
# 초기 개체 생성
def initialize_population(size, num_sides):
return [create_sofa(np.random.randint(3, num_sides)) for _ in range(size)]
# 시각화
def visualize_sofa(sofa_points, corridor):
# ... (생략)
# 메인 함수
if __name__ == "__main__":
corridor = [(0, 0), (1, 1)] # 복도 좌표
population = initialize_population(POPULATION_SIZE, 5) # 초기 개체 생성 (최대 5각형)
best_sofa = genetic_algorithm(population, calculate_fitness, corridor, MAX_ITERATIONS)
visualize_sofa(best_sofa, corridor)
*
import numpy as np
import matplotlib.pyplot as plt
# 상수 정의
CORRIDOR_WIDTH = 1 # 복도 폭
MAX_ITERATIONS = 1000 # 유전 알고리즘 반복 횟수
POPULATION_SIZE = 100 # 개체 수
# 소파 표현 (다각형)
def create_sofa(num_sides):
# ... (생략)
# 소파 회전
def rotate_sofa(points, angle):
# ... (생략)
# 충돌 검사 (복도를 두 개의 직선으로 나누어 검사)
def check_collision(sofa_points, corridor):
# ... (생략)
# 다각형 면적 계산 (가우스의 끈 공식)
def calculate_polygon_area(points):
x = points[:, 0]
y = points[:, 1]
return 0.5 * np.abs(np.dot(x, np.roll(y, 1)) - np.dot(y, np.roll(x, 1)))
# 적합도 함수
def calculate_fitness(sofa_points, corridor):
area = calculate_polygon_area(sofa_points)
if check_collision(sofa_points, corridor):
area *= 0.5
return area
# 유전 알고리즘
def genetic_algorithm(population, fitness_func, corridor, max_iterations):
for generation in range(max_iterations):
# 선택 (토너먼트 선택)
# ...
# 교차
# ...
# 돌연변이
# ...
return max(population, key=lambda x: fitness_func(x, corridor))
# 초기 개체 생성
def initialize_population(size, num_sides):
return [create_sofa(np.random.randint(3, num_sides)) for _ in range(size)]
# 시각화
def visualize_sofa(sofa_points, corridor):
# ... (생략)
# 메인 함수
if __name__ == "__main__":
corridor = [(0, 0), (1, 1)] # 복도 좌표
population = initialize_population(POPULATION_SIZE, 5) # 초기 개체 생성 (최대 5각형)
best_sofa = genetic_algorithm(population, calculate_fitness, corridor, MAX_ITERATIONS)
visualize_sofa(best_sofa, corridor)
일리어스님의 댓글
최대값을 못찾은게 아니라
정확히는 최대값을 찾는 공식을 못찾은거죠.
현재까지의 최대값은 있는데
공식이 없다보니 이게 최대가 맞나.. 더 큰건 없나. 증명을 못한 상황
정확히는 최대값을 찾는 공식을 못찾은거죠.
현재까지의 최대값은 있는데
공식이 없다보니 이게 최대가 맞나.. 더 큰건 없나. 증명을 못한 상황
















제리아스님의 댓글