가장 큰 소수 기록 경신 '4102만 자리 숫자'…읽는 데만 470일
알림
|
페이지 정보
작성일
2024.10.23 17:28
본문
https://damoang.net/free/2001685
2018년 이후 6년 만에 알려진 '가장 큰 소수' 기록 경신
소수 찾기, 당장은 못 써도 전산 암호·난수 생성에 활용
메르센 소수 프로젝트(GIMPS)는 새로운 소수가 검증을 마쳐 알려진 가장 큰 소수 기록이 바뀌었다고 발표했다. 2024.10.23 /뉴스1
(서울=뉴스1) 김승준 기자 = 자릿수가 4102만 이상인 소수가 발견됐다. 이 수는 2의 1억3627만 9841제곱에서 1을 뺀 수다.
23일 과학기술계에 따르면 메르센 소수 프로젝트(GIMPS)는 새로운 소수가 검증을 마쳐 알려진 가장 큰 소수 기록이 바뀌었다고 발표했다.
소수는 1과 자기 자신으로만 나누어떨어지는 수다.
메르센 수는 2의 n 제곱에서 1을 뺀 형태의 수다. 예를 들어 2의 3제곱인 8에서 1을 뺀 7은 메르센 수다.
메르센 수를 간편히 표현하려고 M(n)으로 나타내기도 한다. 2의 3제곱을 이용해 만들어지는 M(3)은 7이고 2의 4제곱에서 1을 뺀 M(4)는 15다.
메르센 수 중 소수인 것을 메르센 소수라고 부른다. 3인 M(2), 7인 M(3), 31인 M(5), 127인 M(7)이 메르센 소수다.
다음 메르센 소수인 M(13)이 되면 8191이 되고 M(17), M(19), M(31)을 지나며 수가 빠르게 커진다. M(31)은 21억 4748만 3647이다.
수가 이렇게 빠르게 커지기 때문에 48번째 메르센 소수는 약 1754만 자리다.
이번에 소수 검증을 마친 M(136279841)은 4102만 4320자리다. 이는 1초에 1자리씩 읽어도 475일이 걸리는 분량이다.
이번 M(136279841)은 알려진 52번째 메르센 소수로 51번째인 M(82589933)은 2018년에 검증됐다.
1996년 설립된 GIMPS는 메르센 소수를 찾으려는 수학자, 애호가들이 모인 단체다. 소수 탐색 알고리즘이 적용된 소프트웨어를 전 세계의 자발적 참여자가 자신의 컴퓨터에 설치해 컴퓨터의 유휴 계산 자원으로 소수 찾기를 돕는다.
이번 소수 찾기에는 전 엔비디아 직원인 루크 듀랜트가 활약했다. 듀랜트는 여러 GPU 서버에서 GIMPS 소프트웨어 제품을 실행하고 유지 관리하는 인프라를 개발했다. 그 결과 17개국에 걸친 수천개의 서버 GPU가 계산에 활용될 수 있었다.
다만 이런 소수는 너무 크기 때문에 실용적 활용이 어렵다. 학술적으로도 거대 소수 발견보다는 소수의 출현 패턴 파악이 더 가치 있는 편이다.
현대의 주요 전산 암호 체계는 소수를 기반으로 한 수학 문제로 만들어졌다. 거대 소수를 알고 있으면 암호화 수준을 높일 수 있어 당장 활용은 어렵더라도 추후 활용될 여지가 있다.
메르센 소수는 비교적 단순한 형태기 때문에 거대소수 탐색에 유리하다.
또 메르센 소수는 '메르센 트위스터'라는 난수 생성 알고리즘에 활용되기도 한다. 메르센 트위스터는 상당한 수준의 무작위성을 보이는 난수를 생성하고 알고리즘 속도가 빨라 많은 프로그래밍 언어의 기본 난수 생성 알고리즘으로 사용된다.
소수 찾기, 당장은 못 써도 전산 암호·난수 생성에 활용
(서울=뉴스1) 김승준 기자 = 자릿수가 4102만 이상인 소수가 발견됐다. 이 수는 2의 1억3627만 9841제곱에서 1을 뺀 수다.
23일 과학기술계에 따르면 메르센 소수 프로젝트(GIMPS)는 새로운 소수가 검증을 마쳐 알려진 가장 큰 소수 기록이 바뀌었다고 발표했다.
소수는 1과 자기 자신으로만 나누어떨어지는 수다.
메르센 수는 2의 n 제곱에서 1을 뺀 형태의 수다. 예를 들어 2의 3제곱인 8에서 1을 뺀 7은 메르센 수다.
메르센 수를 간편히 표현하려고 M(n)으로 나타내기도 한다. 2의 3제곱을 이용해 만들어지는 M(3)은 7이고 2의 4제곱에서 1을 뺀 M(4)는 15다.
메르센 수 중 소수인 것을 메르센 소수라고 부른다. 3인 M(2), 7인 M(3), 31인 M(5), 127인 M(7)이 메르센 소수다.
다음 메르센 소수인 M(13)이 되면 8191이 되고 M(17), M(19), M(31)을 지나며 수가 빠르게 커진다. M(31)은 21억 4748만 3647이다.
수가 이렇게 빠르게 커지기 때문에 48번째 메르센 소수는 약 1754만 자리다.
이번에 소수 검증을 마친 M(136279841)은 4102만 4320자리다. 이는 1초에 1자리씩 읽어도 475일이 걸리는 분량이다.
이번 M(136279841)은 알려진 52번째 메르센 소수로 51번째인 M(82589933)은 2018년에 검증됐다.
1996년 설립된 GIMPS는 메르센 소수를 찾으려는 수학자, 애호가들이 모인 단체다. 소수 탐색 알고리즘이 적용된 소프트웨어를 전 세계의 자발적 참여자가 자신의 컴퓨터에 설치해 컴퓨터의 유휴 계산 자원으로 소수 찾기를 돕는다.
이번 소수 찾기에는 전 엔비디아 직원인 루크 듀랜트가 활약했다. 듀랜트는 여러 GPU 서버에서 GIMPS 소프트웨어 제품을 실행하고 유지 관리하는 인프라를 개발했다. 그 결과 17개국에 걸친 수천개의 서버 GPU가 계산에 활용될 수 있었다.
다만 이런 소수는 너무 크기 때문에 실용적 활용이 어렵다. 학술적으로도 거대 소수 발견보다는 소수의 출현 패턴 파악이 더 가치 있는 편이다.
현대의 주요 전산 암호 체계는 소수를 기반으로 한 수학 문제로 만들어졌다. 거대 소수를 알고 있으면 암호화 수준을 높일 수 있어 당장 활용은 어렵더라도 추후 활용될 여지가 있다.
메르센 소수는 비교적 단순한 형태기 때문에 거대소수 탐색에 유리하다.
또 메르센 소수는 '메르센 트위스터'라는 난수 생성 알고리즘에 활용되기도 한다. 메르센 트위스터는 상당한 수준의 무작위성을 보이는 난수를 생성하고 알고리즘 속도가 빨라 많은 프로그래밍 언어의 기본 난수 생성 알고리즘으로 사용된다.
김승준 기자 ([email protected])
댓글 3
/ 1 페이지
aicasse님의 댓글
거대 소수 아는 것과 암호화 수준을 높이는 것과는 그다지 상관이 없습니다.
암호학에 쓰이는 소수는 무작위성을 가져야 하는데, 메르센 소수는 특별한 구조를 가지고 있는 소수라서 그런 용도 (예를 들어 RSA의 비밀키 생성) 사용이 불가능하죠. 백번 양보해서, 쓸 수 있다고 해도(아닙니다만) 숫자가 커지면 그만큼 그 큰 숫자를 다뤄서 뭔가 일을 하는 데에 드는 시간도 커지기 때문에, 비효율성이 함께 커집니다.
암호에 쓰이는 소수는, 간단히 말해 남이 몰라야 합니다. 하지만 이번에 발견된 메르센 소수는 52번째 숫자죠. 그 앞의 51개가 이미 모든 사람이 아는 목록에 있습니다. 이번에 52번째가 목록에 올라갑니다. 이제 다들 아는 숫자가 되었습니다. 그래서 쓸 수가 없습니다. 53번째 숫자는? 남들도 모르지만, 지금은 아무도 모릅니다. 따라서 역시 쓸 수가 없습니다.
메르센 트위스터에 쓰이는 메르센 소수는 이번에 발견된 것보다 비교할 수 없이 작은 소수를 쓰고, 그걸로도 이미 차고 넘칩니다. 효율성 때문에 쓰는 비암호학적 난수발생기인데, 무지무지 큰 소수를 쓸 이유가 없습니다.
https://www.clien.net/service/board/park/12621556
암호학에 쓰이는 소수는 무작위성을 가져야 하는데, 메르센 소수는 특별한 구조를 가지고 있는 소수라서 그런 용도 (예를 들어 RSA의 비밀키 생성) 사용이 불가능하죠. 백번 양보해서, 쓸 수 있다고 해도(아닙니다만) 숫자가 커지면 그만큼 그 큰 숫자를 다뤄서 뭔가 일을 하는 데에 드는 시간도 커지기 때문에, 비효율성이 함께 커집니다.
암호에 쓰이는 소수는, 간단히 말해 남이 몰라야 합니다. 하지만 이번에 발견된 메르센 소수는 52번째 숫자죠. 그 앞의 51개가 이미 모든 사람이 아는 목록에 있습니다. 이번에 52번째가 목록에 올라갑니다. 이제 다들 아는 숫자가 되었습니다. 그래서 쓸 수가 없습니다. 53번째 숫자는? 남들도 모르지만, 지금은 아무도 모릅니다. 따라서 역시 쓸 수가 없습니다.
메르센 트위스터에 쓰이는 메르센 소수는 이번에 발견된 것보다 비교할 수 없이 작은 소수를 쓰고, 그걸로도 이미 차고 넘칩니다. 효율성 때문에 쓰는 비암호학적 난수발생기인데, 무지무지 큰 소수를 쓸 이유가 없습니다.
https://www.clien.net/service/board/park/12621556
aicasse님의 댓글의 댓글
@aicasse님에게 답글
https://www.mersenne.org/why_join/
왜 메르센 소수를 찾는가에 대한 답은, 위의 신문 기사에서 엉뚱한 이야기를 하는 것과는 달리,
정작 GIMPS 프로젝트 웹사이트에 잘 정리되어 있습니다. 아주 짧게 요약해 보자면,
큰 수를 처리하는 과정에서 알고리즘적인 부산물이 있고, 하드웨어 테스트의 역할도 하고,
수학적, 역사적 전통이고, 하지만 무엇보다 재밌으니까… 정도입니다. 이론적으로나 실제적으로
대단한 의미가 있는 것은 사실 아닙니다. 재밌으니까 한다고 생각하면 됩니다.
그리고, 그걸로 충분합니다. 여기에 굳이 다른 이유와 중요성을 갖다붙일 까닭이 없습니다.
왜 메르센 소수를 찾는가에 대한 답은, 위의 신문 기사에서 엉뚱한 이야기를 하는 것과는 달리,
정작 GIMPS 프로젝트 웹사이트에 잘 정리되어 있습니다. 아주 짧게 요약해 보자면,
큰 수를 처리하는 과정에서 알고리즘적인 부산물이 있고, 하드웨어 테스트의 역할도 하고,
수학적, 역사적 전통이고, 하지만 무엇보다 재밌으니까… 정도입니다. 이론적으로나 실제적으로
대단한 의미가 있는 것은 사실 아닙니다. 재밌으니까 한다고 생각하면 됩니다.
그리고, 그걸로 충분합니다. 여기에 굳이 다른 이유와 중요성을 갖다붙일 까닭이 없습니다.
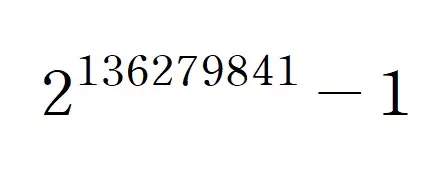
하늘만이님의 댓글
다 읽었더니 2026년?